2D Truss Solver
Quarta atividade prática supervisionada de Transferência de calor e mecânica dos sólidos, com objetivo de fazer um solver para treliças planas.
| Home |
|---|
| Sobre o Projeto |
| Baixando o Projeto |
APS 4: PROJETO DE SOFTWARE PARA ANÁLISE DE TRELIÇAS PLANAS
1. OBJETIVO GERAL
O objetivo da atividade é desenvolver um software para análise de treliças planas.
2. RUBRICA
- O código deverá ser desenvolvido em Python de modo que os dados de entrada possam ser facilmente alterados a partir de uma planilha como descrito no Anexo 1.
- O código deverá aplicar técnicas numéricas para solução de sistemas de equações (Método de Jacobi e/ou Gauss-Seidel).
- O código deverá gerar um arquivo de saída com o pós-processamento dos dados de acordo com modelo descrito no Anexo 1.
- O código deverá ser desenvolvido para aplicação geral em treliças 2D. Para isso, o grupo deverá validar os dados de saída, usando a estrutura indicada no Anexo 2.
ANEXO 1
A seguir apresentamos um modelo de arquivo de entrada para análise da treliça ilustrada na Fig. 1.
Treliça com 3 elementos de Barra
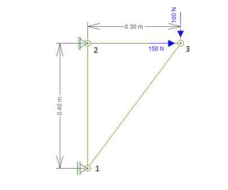
Especificações das Barras
Cada barra do exemplo possui as seguintes características:
- Área de seção transversal (A):
2 × 10^-4 m² - Módulo de elasticidade (E):
210 GPa
Cargas Aplicadas
As cargas pontuais aplicadas são:
- No nó 3, direção y:
P_y = -100 N - Na direção x:
P_x = 150 N
Tensões Ultimate
As tensões últimas tanto para tração quanto para compressão são:
- Tensão última à tração (σₜₐₓₐçãₒ):
1570 × 10^3 Pa - Tensão última à compressão (σₜₐₓₐₘₑₙₜₒ):
1570 × 10^3 Pa
Arquivo de entrada
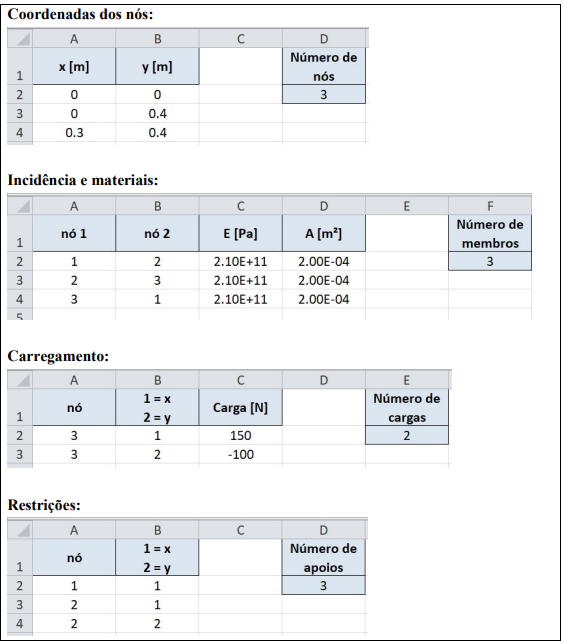
Arquivo de saída

Pós Processamento da Treliça plana com 3 elementos
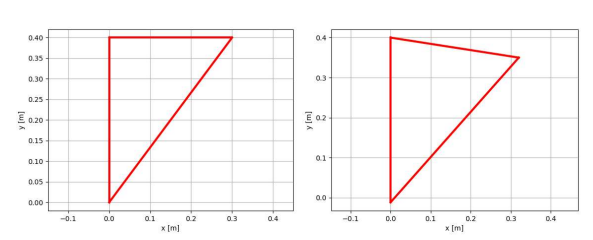
A figura ilustra o pós-processamento para a análise da treliça plana com três elementos. (Esquerda) Treliça antes da aplicação das forças. (Direita) Treliça após a aplicação das forças.
ANEXO 2
Considere a estrutura ilustrada abaixo para validação do software desenvolvido. Adote a numeração indicada para os nós e elementos.
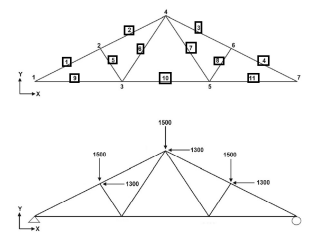
Descrição do Modelo
- Estrutura bidimensional e conectada por juntas do tipo rótula (Treliça).
- Estrutura pinada na esquerda, e apoiada na extremidade direita.
Material: AISI 310 Stainless Steel (SS)
Propriedades Mecânicas:
- Módulo de Elasticidade (E):
193.14 GPa - Área de Seção Transversal (A):
5.25 mm²
Coordenadas dos Nós
| Nó | x [mm] | y [mm] |
|---|---|---|
| 1 | 0 | 72 |
| 2 | 144 | 144 |
| 3 | 192 | 0 |
| 4 | 288 | 72 |
| 5 | 384 | 0 |
| 6 | 432 | 72 |
| 7 | 576 | 0 |
BIBLIOGRAFIA:
- BITTENCOURT, M.L. COMPUTATIONAL SOLID MECHANICS: VARIATIONAL FORMULATION AND HIGH ORDER APPROXIMATION, 6A EDIÇÃO, CRC PRESS, 2014.
- CHAPRA, STEVEN C.; CANALE, RAYMOND P. NUMERICAL METHODS FOR ENGINEERS. 6TH ED. NEW YORK: MCGRAW-HILL HIGHER EDUCATION, C2010. 968 P. ISBN 978007340106 (ENC.)
- NOTAS DE AULA E TEXTOS FORNECIDOS AO LONGO DO SEMESTRE.